Quadratische Gleichungen

1. Was sind quadratische Gleichungen?

Quadratische Gleichungen sind mathematische Probleme, die ihre Ordnung 2 beträgt. Die Form einer quadratischen Gleichung ist :

𝑎 . 𝑥² + 𝑏. 𝑥 + 𝑐 = 0

Die größte Ordnung der Variable x beträgt 2. a, b und c sind konstante Zahlen. Sie können positiv oder auch negativ sein. Z. B.

2 . 𝑥² + 5. 𝑥 + 3 = 0

In dieser Gleichung ist der Koeffizient a = 2, b = 5 und c = 3

𝑥² − 5. 𝑥 + 1 = 0

In der zweiten Gleichung ist der Koeffizient a = 1, b = -5 und c = 1

2. Lösung einer quadratischen Gleichung

Eine quadratische Gleichung hat zwei Lösungen x₁ und x₂. Es gibt verschiedene Methoden zur Ermittlung der Werte von x₁ und x₂. In Bestimmten Fällen gibt es nur eine einzige Lösung. Es kann auch sein die Gleichung keine Lösung hat. Um herauszufinden, welchen Fall vorliegt, wird die Diskriminante Methode verwendet.

2.1 Diskriminante Methode D:

D kann wie folgt berechnet werden

𝐷= 𝑏² −4.𝑎.𝑐

𝐷 > 0 ⟹ Es gibt zwei Lösungen für die quadratische Gleichung.

Die Lösungen sind durch die Mitternachtsformel definiert

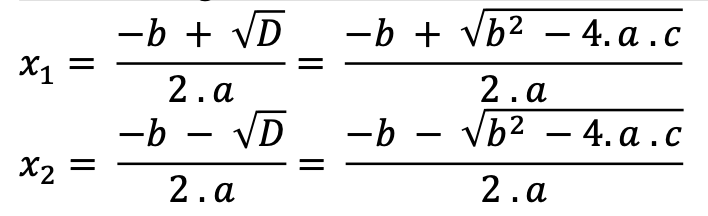
𝐷 = 0 ⟹ Es gibt eine Lösung für die quadratische Gleichung

𝐷 < 0 ⟹ Es gibt keine Lösungen für die quadratische Gleichung in der Menge der reellen Zahlen

2.2 pq-Formel:

Die pq-Formel kann für quadratische Gleichungen der Form

𝑥² + 𝑝 . 𝑥 + 𝑞 = 0

verwendet werden. Der Koeffizient vor x² muss a = 1 sein. Wenn das nicht der Fall ist, muss die Gleichung umgeformt werden und dann die pq-Formel verwenden.

Die Lösung mit der pq-Formel lautet:

3. Beispiele:

3.1 Beispiel
2.𝑥² −5.𝑥 +2=0

Hier ist die größte Ordnung für die Variable x. x² Ordnung = 2, a = 2, b = -5 und c = 2

Lösung mit der Diskriminante Methode D und Mitternachsformel:

𝐷= 𝑏² −4.𝑎.𝑐
𝐷 = (−5)² −4 . 2 .2
𝐷=25 −16=9>0 ⟹𝐸𝑠𝑔𝑖𝑏𝑡𝑧𝑤𝑒𝑖𝐿ö𝑠𝑢𝑛𝑔𝑒𝑛

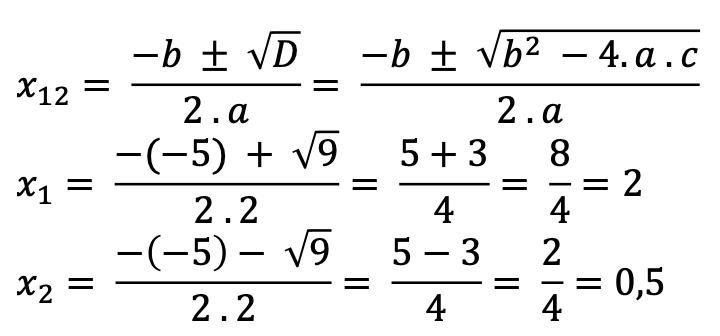
Die Gleichung kann auch mit der pq-Formel gelöst werden, jedoch ist dafür ein Umformungsschritt notwendig, da der Vorfaktor für die Variable x² gleich 2 ist. Zunächst muss die Gleichung durch den Vorfaktor 2 geteilt werden, bevor die Formel angewendet werden kann.

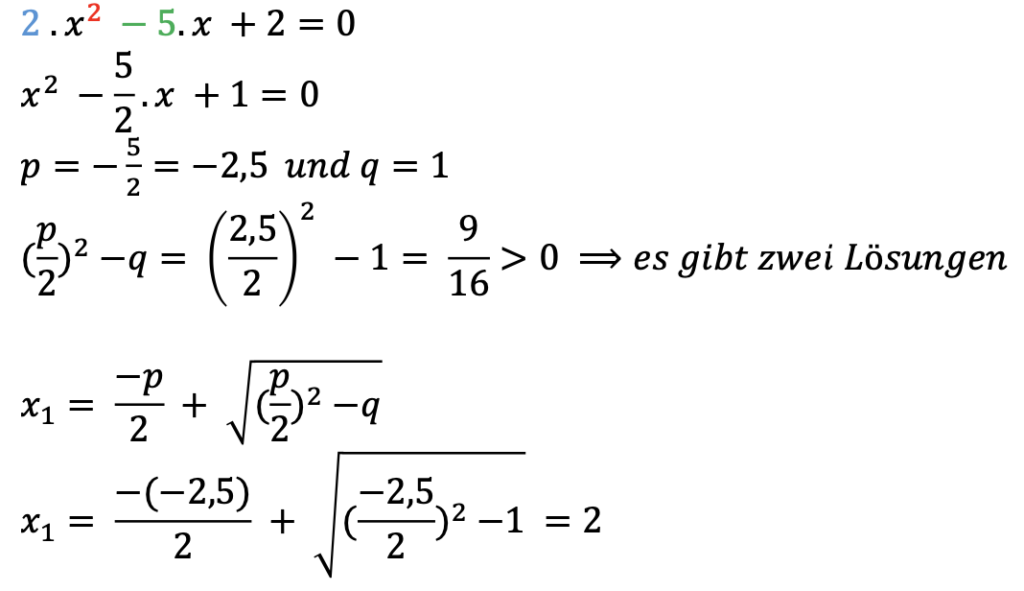
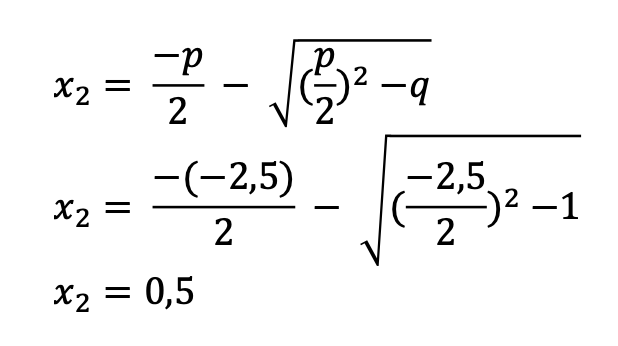
3.2 Beispiel

𝑥² − 2 = 0
Hier ist die größte Ordnung für die Variable x. x² Ordnung = 2, a = 1, b = 0 und c = -2

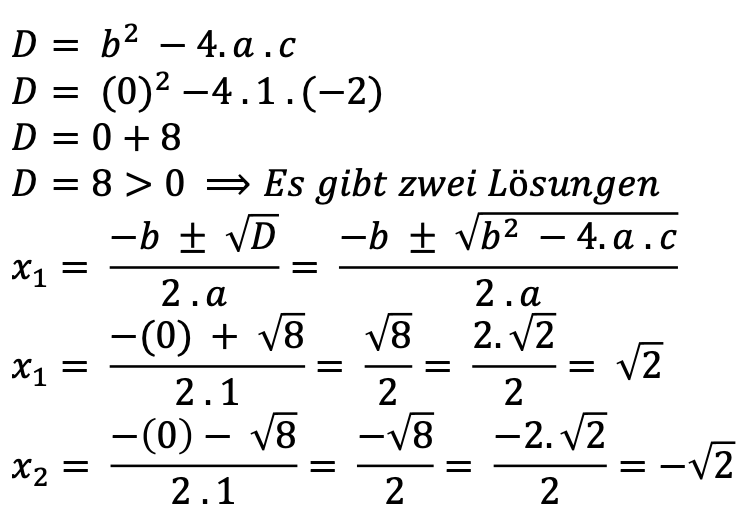
Die Gleichung kann auch direkt mit der pq-Formel gelöst werden

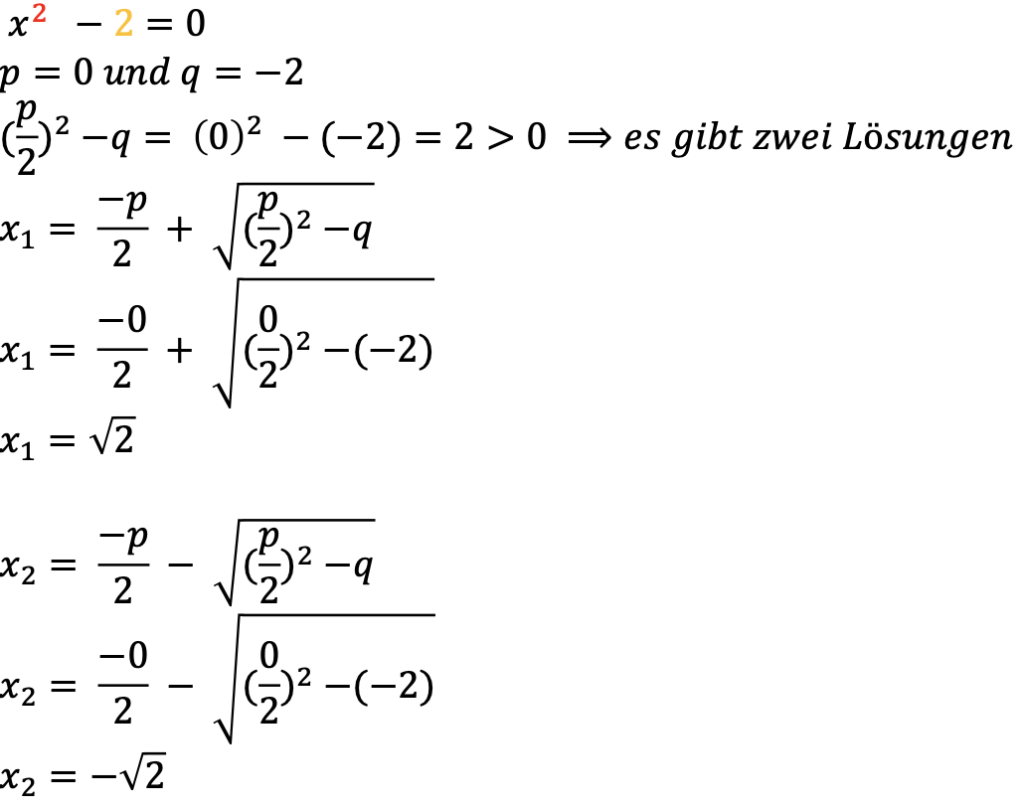
4. Grafische Darstellung

Die Lösungen einer quadratischen Gleichung sind Nullstellen der Funktion Zunächst ist die Gleichung aus dem Beispiel 3.1 dargestellt

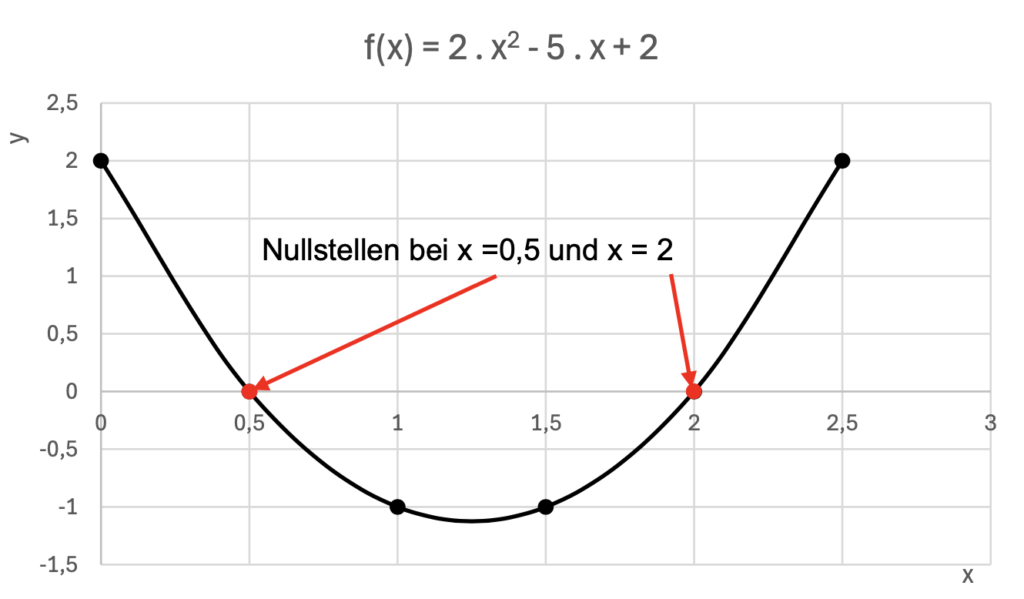
Grafische Darstellung für die Gleichung aus dem Beispiel 3.2